Giải toán 6 Bài 11 Ước chung. Ước chung lớn nhất trang 44 – KNTT

Trang 44 của sách “Giải toán 6” trong bộ sách “Kết nối tri thức” giúp học sinh nắm vững kiến thức về ước chung. Ước chung lớn nhất. Bài 11 cung cấp các phương pháp phân tích số ra thừa số nguyên tố, tìm ước chung và ước chung lớn nhất một cách chi tiết và dễ hiểu. Thông qua các bài tập thực hành, học sinh sẽ rèn luyện kỹ năng giải toán và phát triển tư duy logic một cách hiệu quả.

Giải toán 6 Bài 11 Ước chung. Ước chung lớn nhất trang 44

Câu 2.30 trang 48 toán 6 kết nối tri thức

Tìm tập hợp ước chung của:

a) 30 và 45;

b) 42 và 70.

Đáp án: 

Để tìm tập hợp ước chung của hai số, ta sẽ tìm các ước của từng số rồi lấy giao của hai tập hợp này.

a) Ước chung của 30 và 45

Ước của 30: 30 = 2 × 3 × 5

• Các ước của 30: 1, 2, 3, 5, 6, 10, 15, 30

Ước của 45: 45 = 3² × 5

• Các ước của 45: 1, 3, 5, 9, 15, 45

Ước chung của 30 và 45:

• Giao của hai tập hợp ước: 1, 3, 5, 15

Vậy, tập hợp ước chung của 30 và 45 là:$$\{1,3,5,15\}$$

b) Ước chung của 42 và 70

Ước của 42: 42 = 2 × 3 × 7

• Các ước của 42: 1, 2, 3, 6, 7, 14, 21, 42

Ước của 70: 70 = 2 × 5 × 7

• Các ước của 70: 1, 2, 5, 7, 10, 14, 35, 70

Ước chung của 42 và 70:

• Giao của hai tập hợp ước: 1, 2, 7, 14

Vậy, tập hợp ước chung của 42 và 70 là:

$$\{1,2,7,14\}$$

Kết luận

• Tập hợp ước chung của 30 và 45 là $\{1, 3, 5, 15\}$
  
• Tập hợp ước chung của 42 và 70 là $\{1, 2, 7, 14\}$
  

Câu 2.31 trang 48 toán 6 kết nối tri thức

Tìm ƯCLN của hai số:

a) 40 và 70;

b) 55 và 77.

Đáp án: 

a) ƯCLN của 40 và 70

Phân tích ra thừa số nguyên tố:

• 40 = $2^3 \times 5$
  
• 70 = $2 \times 5 \times 7$
  

Các thừa số nguyên tố chung của 40 và 70:

• Thừa số chung: 2 và 5

Lấy tích của các thừa số nguyên tố chung với số mũ nhỏ nhất:

• Số mũ nhỏ nhất của 2 là 1.
• Số mũ nhỏ nhất của 5 là 1.

Vậy, ƯCLN của 40 và 70 là: $\text{ƯCLN}(40, 70) = 2^1 \times 5^1 = 2 \times 5 = 10$

b) ƯCLN của 55 và 77

Phân tích ra thừa số nguyên tố:

• 55 = $5 \times 11$
  
• 77 = $7 \times 11$
  

Các thừa số nguyên tố chung của 55 và 77:

• Thừa số chung: 11

Lấy tích của các thừa số nguyên tố chung với số mũ nhỏ nhất:

• Số mũ nhỏ nhất của 11 là 1.

Vậy, ƯCLN của 55 và 77 là: $\text{ƯCLN}(55, 77) = 11$

Câu 2.32 trang 48 toán 6 kết nối tri thức

Tìm ƯCLN của:

a) 22.5 và 2. 3. 5;

b) 24.3; 22.32.5 và 24.11

Đáp án:

a) 22.5 và 2. 3. 5

Ta thấy 2 và 5 là thừa số nguyên tố chung. Số mũ nhỏ nhất của 2 là 1 và số mũ nhỏ nhất của 5 là 1 nên

ƯCLN cần tìm là 2.5 = 10.

b) 24.3; 22.32.5 và 24.11

Ta thấy 2 là thừa số nguyên tố chung. Số mũ nhỏ nhất của 2 là 2 nên
ƯCLN cần tìm là 22 = 4

Câu 2.33 trang 48 toán 6 kết nối tri thức

Cho hai số a = 72 và b = 96

a) Phân tích a và b ra thừa số nguyên tố;

b) Tìm ƯCLN(a, b), rồi tìm ƯC(a, b).

Đáp án: 

a) Phân tích a và b ra thừa số nguyên tố

• Số $a = 72$
  

$72 = 2^3 \times 3^2$

• Số $b = 96$
  

$96 = 2^5 \times 3$

b) Tìm ƯCLN(a, b) và ƯC(a, b)

Ước chung lớn nhất (ƯCLN):

Để tìm ƯCLN của hai số, ta lấy các thừa số nguyên tố chung với số mũ nhỏ nhất.

• Thừa số chung của 72 và 96 là 2 và 3.
• Số mũ nhỏ nhất của 2 là 3.
• Số mũ nhỏ nhất của 3 là 1.

Do đó:

$\text{ƯCLN}(72, 96) = 2^3 \times 3 = 8 \times 3 = 24$

Ước chung (ƯC):

Ước chung của hai số $a$ và $b$ là tập hợp các số chia hết cho ƯCLN(a, b).

• Các ước của ƯCLN(24) là: 1, 2, 3, 4, 6, 8, 12, 24.

Câu 2.34 trang 48 toán 6 kết nối tri thức

Các phân số sau đã là phân số tối giản chưa? Nếu chưa, hãy rút gọn về phân số tối giản?

a) 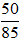  ;                     b)  .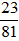

Đáp án: 

a) Ta có:

50 = 2.5²;           85 = 5.17

+) Thừa số nguyên tố chung là 5 với số mũ nhỏ nhất là 1 nên ƯCLN(50, 85) = 5.

Do đó 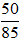 không là phân số tối giản.

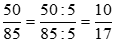 . Ta được  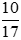là phân số tối giản vì ƯCLN(10, 17) = 1.

b) Ta có:

23 = 23;           81 = 3⁴

Nên 23 và 81 không có thừa số nguyên tố chung nên ƯCLN(23, 81) = 1.

Do đó 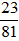 là phân số tối giản.

Câu 2.35 trang 48 toán 6 kết nối tri thức

Hãy cho hai ví dụ về hai số có ƯCLN bằng 1 mà cả hai đều là hợp số.

Đáp án: 

Dưới đây là hai ví dụ về các cặp số có ƯCLN bằng 1 và cả hai đều là hợp số:

Ví dụ 1

Số 1: 14 (hợp số, vì $14 = 2 \times 7$)

Số 2: 15 (hợp số, vì $15 = 3 \times 5$)

• ƯCLN của 14 và 15 là 1.

Ví dụ 2

Số 1: 35 (hợp số, vì $35 = 5 \times 7$)

Số 2: 36 (hợp số, vì $36 = 2^2 \times 3^2$)

• ƯCLN của 35 và 36 là 1.

Xem thử: Giải toán 6 Luyện tập chung trang 43 – Kết nối tri thức