Tiên đề Euclid…thẳng song song là một trong những nền tảng cơ bản nhất của hình học, đặt ra mối liên hệ giữa các đường thẳng và khái niệm về không gian. Trong chương này của sách giáo khoa Toán 7 Kết nối tri thức, chúng ta sẽ khám phá sâu hơn về Tiên đề Euclid, cách nó định hình các lý thuyết toán học và ứng dụng của nó trong việc giải quyết các bài toán liên quan đến đường thẳng song song, giúp học sinh hiểu rõ và vận dụng hiệu quả trong các bài tập và trong thực tế.
Giải bài tiên đề Euclid. Tính chất của hai đường thẳng song song
Bài 3.17 toán 7 sgk KNTT trang 53
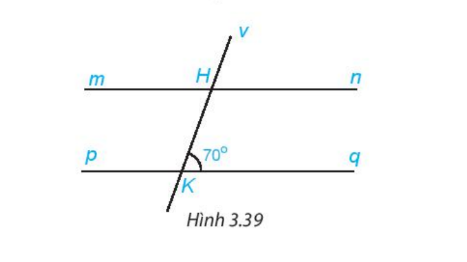
Cho Hình 3.39, biết rằng \( mn \parallel pq \). Tính số đo các góc \( \widehat{mHK} \) và \( \widehat{vHn} \).
Giải:
Dựa vào Hình 3.39, ta có:
\[
mn \parallel pq.
\]
Và biết rằng góc \( \widehat{K} = 70^\circ \).
Tính góc \( \widehat{mHK} \): Do \( mn \parallel pq \), góc \( \widehat{K} \) và góc \( \widehat{mHK} \) là hai góc so le trong, vì vậy:
\[
\widehat{mHK} = \widehat{K} = 70^\circ.
\]
Tính góc \( \widehat{vHn} \): Góc \( \widehat{vHn} \) và góc \( \widehat{mHK} \) là hai góc đối đỉnh, do đó chúng bằng nhau:
\[
\widehat{vHn} = \widehat{mHK} = 70^\circ.
\]
Kết luận:
\[
\widehat{mHK} = 70^\circ \quad \text{và} \quad \widehat{vHn} = 70^\circ.
\]
Bài 3.18 toán 7 sgk KNTT trang 53
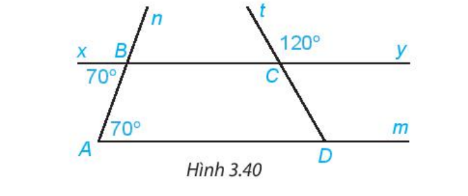
Cho Hình 3.40.
Giải:
(a) Giải thích tại sao \( Am \parallel By \):
Dựa vào hình vẽ, ta có:
\[
\widehat{B} = 70^\circ \quad \text{và} \quad \widehat{A} = 70^\circ.
\]
Hai góc \( \widehat{B} \) và \( \widehat{A} \) là hai góc so le trong được tạo thành bởi các đường thẳng \( Am \) và \( By \) khi bị cắt bởi đường thẳng \( AB \). Theo tính chất của góc so le trong, nếu hai góc so le trong bằng nhau thì hai đường thẳng đó song song. Vì vậy, ta có:
\[
Am \parallel By.
\]
(b) Tính số đo góc \( \widehat{CDm} \):
Ta có:
\( Am \parallel By \) do hai góc so le trong \( \widehat{B} \) và \( \widehat{A} \) bằng nhau.
Số đo của góc \( \widehat{CDm} \) là \( 120^\circ \).
Bài 3.19 toán 7 sgk KNTT trang 54
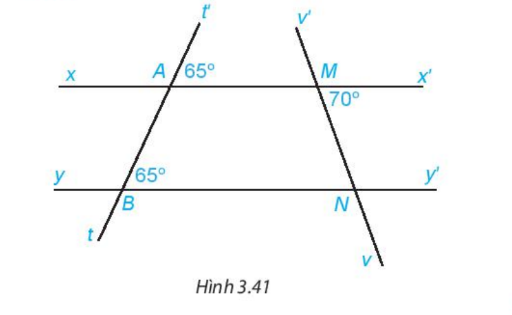
Cho Hình 3.41.
Giải:
(a) Giải thích tại sao \( xx’ \parallel yy’ \):
Dựa vào hình vẽ, ta có các góc \( \widehat{A} = 65^\circ \) và \( \widehat{B} = 65^\circ \).
Hai góc \( \widehat{A} \) và \( \widehat{B} \) là hai góc so le trong do đường thẳng \( AB \) cắt hai đường thẳng \( xx’ \) và \( yy’ \). Theo tính chất của góc so le trong, nếu hai góc so le trong bằng nhau thì hai đường thẳng đó song song. Vì vậy, ta có:
\[
xx’ \parallel yy’.
\]
(b) Tính số đo góc \( \widehat{MNB} \):
Ta có:
\( xx’ \parallel yy’ \) do hai góc so le trong \( \widehat{A} \) và \( \widehat{B} \) bằng nhau.
Số đo của góc \( \widehat{MNB} \) là \( 70^\circ \).
Bài 3.20 toán 7 sgk KNTT trang 54
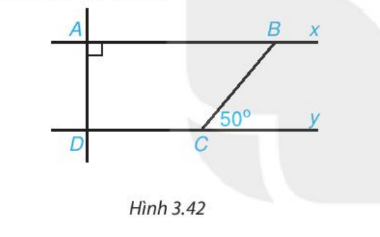
Cho Hình 3.42, biết rằng \( Ax \parallel Dy \), \( \widehat{A} = 90^\circ \), và \( \widehat{BCy} = 50^\circ \). Tính số đo các góc \( \widehat{ADC} \) và \( \widehat{ABC} \).
Giải:
Tính số đo góc \( \widehat{ADC} \):
Do \( Ax \parallel Dy \) và \( AD \) là đường vuông góc với \( Dy \), ta có:
\[
\widehat{ADC} = 90^\circ.
\]
Tính số đo góc \( \widehat{ABC} \):
Góc \( \widehat{BCy} = 50^\circ \) là góc kề bù với góc \( \widehat{ABC} \), vì vậy:
\[
\widehat{ABC} = \widehat{BCy} = 50^\circ
\]
Kết luận:
Số đo góc \( \widehat{ADC} = 90^\circ \).
Số đo góc \( \widehat{ABC} = 50^\circ \).
Xem thêm bài giải: “Toán 7 Kết nối tri thức 1: Luyện tập chung trang 50“.
Bài 3.21 toán 7 sgk KNTT trang 54
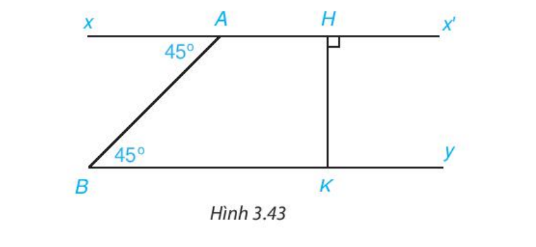
Cho Hình 3.43. Giải thích tại sao:
Giải:
(a) Giải thích tại sao \( Ax’ \parallel By \):
Dựa vào hình vẽ, ta có góc \( \widehat{A} = 45^\circ \) và góc \( \widehat{B} = 45^\circ \). Hai góc này là hai góc so le trong do đường thẳng \( AB \) cắt hai đường thẳng \( Ax’ \) và \( By \). Theo tính chất của góc so le trong, nếu hai góc này bằng nhau thì hai đường thẳng \( Ax’ \) và \( By \) là song song.
Vì vậy, ta có:
\[
Ax’ \parallel By.
\]
(b) Giải thích tại sao \( By \perp HK \):
Dựa vào hình vẽ, \( HK \) là đường thẳng vuông góc với \( x’ \), tức là góc \( \widehat{HK} = 90^\circ \). Do đó, \( By \) cũng vuông góc với \( HK \), vì \( By \) là đường thẳng song song với \( Ax’ \). Từ đó, ta có:
\[
By \perp HK.
\]
Kết luận:
\( Ax’ \parallel By \) do hai góc so le trong \( \widehat{A} \) và \( \widehat{B} \) bằng nhau.
\( By \perp HK \) vì góc giữa chúng là \( 90^\circ \).
Bài 3.22 toán 7 sgk KNTT trang 54
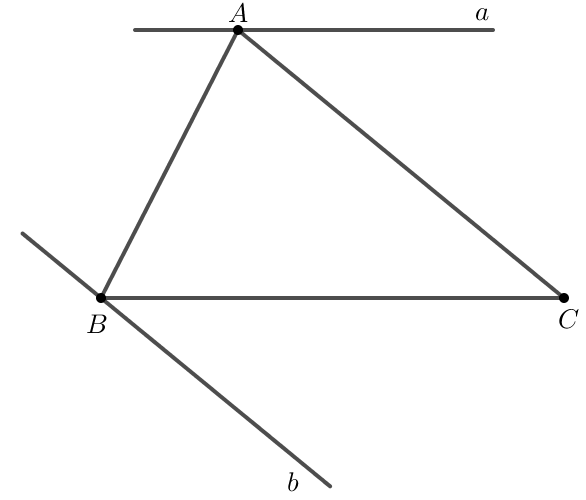
Cho tam giác \( ABC \). Vẽ đường thẳng \( a \) đi qua \( A \) và song song với \( BC \). Vẽ đường thẳng \( b \) đi qua \( B \) và song song với \( AC \). Có thể vẽ được bao nhiêu đường thẳng \( a \), bao nhiêu đường thẳng \( b \)? Vì sao?
Giải:
Đường thẳng \( a \) đi qua điểm \( A \) và song song với \( BC \):
Theo định lý về đường thẳng song song, chỉ có thể vẽ được duy nhất một đường thẳng \( a \) đi qua điểm \( A \) và song song với \( BC \). Điều này là do qua một điểm ngoài một đường thẳng, chỉ có thể vẽ duy nhất một đường thẳng song song với đường thẳng đã cho.
Đường thẳng \( b \) đi qua điểm \( B \) và song song với \( AC \):
Tương tự, chỉ có thể vẽ được duy nhất một đường thẳng \( b \) đi qua điểm \( B \) và song song với \( AC \). Điều này cũng dựa trên định lý về đường thẳng song song, rằng qua một điểm ngoài một đường thẳng, chỉ có thể vẽ duy nhất một đường thẳng song song với đường thẳng đó.
Kết luận:
Có thể vẽ được duy nhất một đường thẳng \( a \) đi qua \( A \) và song song với \( BC \).
Có thể vẽ được duy nhất một đường thẳng \( b \) đi qua \( B \) và song song với \( AC \).
Bài 3.23 toán 7 sgk KNTT trang 54
Cho Hình 3.44. Giải thích tại sao:
Giải:
(a) Giải thích tại sao \( MN \parallel EF \):
Xét tam giác \( \triangle DEF \), ta có:
\[
\widehat{EMN} = 30^\circ, \quad \widehat{EFM} = 30^\circ.
\]
Hai góc này bằng nhau, và cùng thuộc các đoạn thẳng \( MN \) và \( EF \), do đó theo định lý về các góc so le trong, \( MN \parallel EF \).
(b) Giải thích tại sao \( HK \parallel EF \):
Tương tự, xét tam giác \( \triangle DEF \) với các góc tại \( H \) và \( K \), ta có:
\[
\widehat{HKE} = 60^\circ, \quad \widehat{EHK} = 60^\circ.
\]
Hai góc này bằng nhau và cùng thuộc các đoạn thẳng \( HK \) và \( EF \), do đó theo định lý về các góc so le trong, \( HK \parallel EF \).
(c) Giải thích tại sao \( HK \parallel MN \):
Cuối cùng, do \( HK \parallel EF \) và \( MN \parallel EF \), theo tính chất của các đường thẳng song song, ta có:
\[
HK \parallel MN.
\]
Kết luận:
\( MN \parallel EF \) do các góc so le trong bằng nhau.
\( HK \parallel EF \) do các góc so le trong bằng nhau.
\( HK \parallel MN \) do chúng đều song song với \( EF \).








