Toán 7 Kết nối tri thức 1: Luyện tập chung trang 58

Phần luyện tập chung trang 58 của sách giáo khoa Toán 7 Kết nối tri thức cung cấp một loạt các bài tập thực hành để học sinh có thể củng cố kiến thức và kỹ năng đã học. Trong bài viết này, chúng ta sẽ phân tích từng bài tập, giải thích chi tiết cách tiếp cận và giải quyết, qua đó giúp các em học sinh không chỉ hiểu sâu các khái niệm toán học mà còn nâng cao kỹ năng giải toán, chuẩn bị tốt nhất cho các bài kiểm tra và thử thách sắp tới.

Giải bài luyện tập chung trang 58

Bài 3.27 toán 7 sgk KNTT trang 58

Cho hình thang \( ABCD \) có cạnh \( AD \) vuông góc với hai đáy \( AB \) và \( CD \). Số đo góc ở đỉnh \( B \) gấp đôi số đo góc ở đỉnh \( C \). Tính số đo các góc của hình thang đó.

Giải:

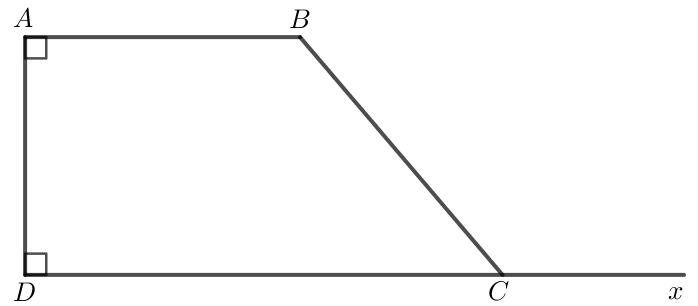
Gọi số đo góc ở đỉnh \( C \) là \( \widehat{C} = \alpha \). Theo đề bài, số đo góc ở đỉnh \( B \) là \( \widehat{B} = 2\alpha \).

Vì \( AD \perp AB \) và \( AD \perp CD \), ta có:
\[
\widehat{A} = \widehat{D} = 90^\circ.
\]

Tổng các góc trong tứ giác là:
\[
\widehat{A} + \widehat{B} + \widehat{C} + \widehat{D} = 360^\circ.
\]

Thay các giá trị đã biết vào phương trình trên:
\[
90^\circ + 2\alpha + \alpha + 90^\circ = 360^\circ.
\]

Tính toán:
\[
180^\circ + 3\alpha = 360^\circ.
\]

Suy ra:
\[
3\alpha = 180^\circ.
\]
\[
\alpha = 60^\circ.
\]

Vậy số đo các góc là:
\[
\widehat{C} = 60^\circ, \quad \widehat{B} = 120^\circ, \quad \widehat{A} = 90^\circ, \quad \widehat{D} = 90^\circ.
\]

Kết luận: Số đo các góc của hình thang \( ABCD \) là:
\[
\widehat{A} = 90^\circ, \quad \widehat{B} = 120^\circ, \quad \widehat{C} = 60^\circ, \quad \widehat{D} = 90^\circ.
\]

Bài 3.28 toán 7 sgk KNTT trang 58

Vẽ hình minh họa và viết giả thiết, kết luận của định lý: “Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau”.

Giải:

Hình minh họa cho định lý hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba.

Giải thích:

– Trong hình minh họa, hai đường thẳng \( d_1 \) và \( d_2 \) lần lượt vuông góc với đường thẳng \( d_3 \).
– Do đó, theo định lý về hai đường thẳng cùng vuông góc với một đường thẳng thứ ba, ta có \( d_1 \parallel d_2 \).

Kết luận: Nếu hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba, thì hai đường thẳng đó song song với nhau.

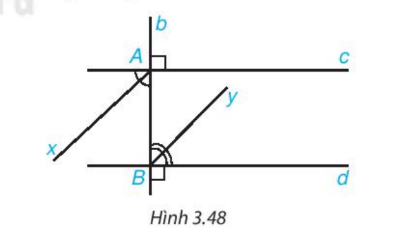
Bài 3.29 toán 7 sgk KNTT trang 58

Kẻ các tia phân giác \( Ax \), \( By \) của một cặp góc so le trong tạo bởi đường thẳng \( b \) vuông góc với hai đường thẳng song song \( c \), \( d \). Chứng minh rằng hai tia phân giác đó nằm trên hai đường thẳng song song.

Giải:

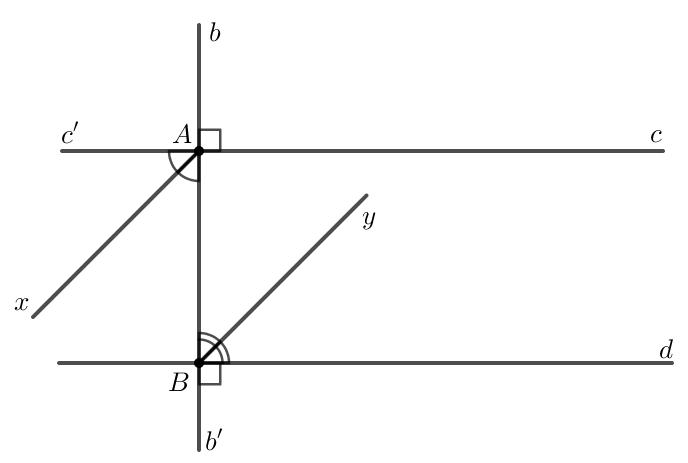
Xét \( AC’ \) là tia đối của tia \( AC \), \( Bb’ \) là tia đối của tia \( BA \). Do đó, ta có \( \angle BAc’ = \angle CAb = 90^\circ \) vì chúng là hai góc đối đỉnh.

Vì \( Ax \) là tia phân giác của \( \angle BAc’ \), nên \( \angle BAx = \frac{1}{2}\angle BAc’ = \frac{1}{2} \times 90^\circ = 45^\circ \).

Xét hai góc kề bù \( \angle dBA \) và \( \angle dBb’ \) có tổng là \( 180^\circ \). Từ đó, ta tính được \( \angle dBA = 180^\circ – \angle dBb’ = 180^\circ – 90^\circ = 90^\circ \).

Tương tự, \( By \) là tia phân giác của \( \angle dBA \), do đó \( \angle ABy = \frac{1}{2} \angle dBA = \frac{1}{2} \times 90^\circ = 45^\circ \).

Như vậy, \( \angle BAx = \angle ABy = 45^\circ \) cho thấy hai góc này bằng nhau và do đó chứng tỏ \( Ax \) song song với \( By \).

Vậy ta đã chứng minh được điều phải chứng minh.

Tham khảo bài sau: “Toán 7 Kết nối tri thức 1: Định lí và chứng minh định lí“.

Bài 3.30 toán 7 sgk KNTT trang 58

Cho hai đường thẳng phân biệt \( a \), \( b \) cùng vuông góc với đường thẳng \( c \); \( d \) là một đường thẳng khác \( c \) và \( d \) vuông góc với \( a \). Chứng minh rằng:
(a) \( a \parallel b \);
(b) \( c \parallel d \);
(c) \( b \perp d \).

Giải:

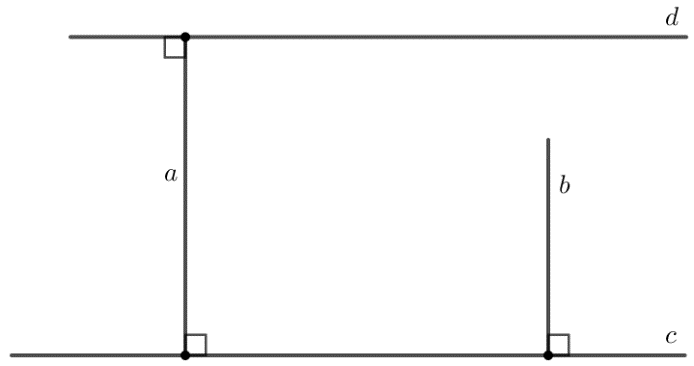
Giả thiết:
Hai đường thẳng \( a \) và \( b \) vuông góc với đường thẳng \( c \).
Đường thẳng \( d \) vuông góc với đường thẳng \( a \).

Chứng minh:

(a) Chứng minh \( a \parallel b \):

Vì \( a \) và \( b \) đều vuông góc với đường thẳng \( c \), theo định lý về hai đường thẳng cùng vuông góc với một đường thẳng thì chúng song song với nhau, ta có:
\[
a \parallel b.
\]

(b) Chứng minh \( c \parallel d \):

Vì \( d \) vuông góc với đường thẳng \( a \), và \( a \parallel b \), nên \( d \) cũng phải vuông góc với \( b \). Do đó, theo định lý về góc vuông, \( c \parallel d \).

(c) Chứng minh \( b \perp d \):

Từ các chứng minh trên, ta đã biết rằng \( d \) vuông góc với \( a \), và vì \( a \parallel b \), nên \( d \) cũng vuông góc với \( b \).
\[
b \perp d.
\]

Bài 3.31 toán 7 sgk KNTT trang 58

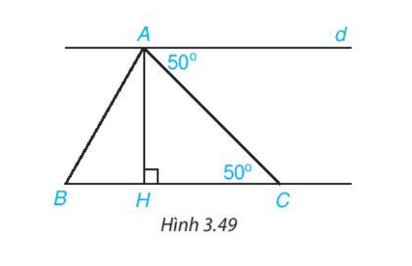
Cho Hình 3.49. Chứng minh rằng:
(a) \( d \parallel BC \);
(b) \( d \perp AH \);
(c) Trong các kết luận trên, kết luận nào được suy ra từ tính chất của hai đường thẳng song song, kết luận nào được suy ra từ dấu hiệu nhận biết hai đường thẳng song song?

Giải:

a) Vì \( \angle DAC \) và \( \angle ACH \) đều bằng \( 50^\circ \), và hai góc này là góc so le trong, nên suy ra \( d \parallel BC \).

b) Theo định lý: “Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại”, và vì \( BC \perp AH \) và \( BC \parallel d \), suy ra \( d \perp AH \).

c) Từ hai nhận xét trên, ta có \( d \parallel BC \) và \( d \perp AH \). Điều này cho thấy \( d \) vừa song song vừa vuông góc với \( AH \), chứng tỏ tính chất đặc biệt của hai đường thẳng song song.