Giải toán 6 Luyện tập chung trang 54 – Kết nối tri thức

“Giải toán 6” của bộ sách “Kết nối tri thức” mang đến những bài luyện tập chung trang 54  đa dạng giúp học sinh củng cố và nâng cao kỹ năng giải các bài toán liên quan đến các khái niệm toán học cơ bản như ƯCLN, BCNN, phân số và các phép tính cơ bản. Các bài tập được thiết kế nhằm khuyến khích học sinh phát triển tư duy logic và khả năng áp dụng kiến thức vào thực tế, qua đó chuẩn bị tốt cho các chương trình học tiếp theo và nâng cao hiểu biết về toán học.

Giải toán 6 Luyện tập chung trang 54

Câu 2.45 trang 55 toán 6 kết nối tri thức

Cho bảng sau:

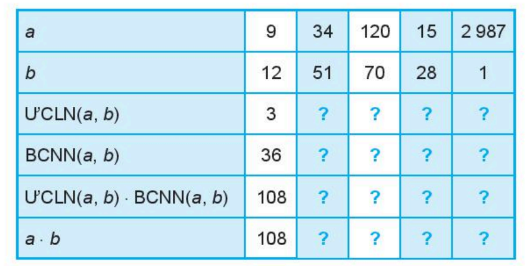
a) Tìm các số thích hợp thay vào ô trống trong bảng;

b) So sánh tích ƯCLN(a, b) . BCNN(a, b) và a.b.

Em rút ra kết luận gì?

Đáp án: 

a) Tìm các số thích hợp thay vào ô trống trong bảng

Ta sẽ điền các số thích hợp vào bảng bằng cách tìm ƯCLN và BCNN của từng cặp số $a$ và $b$.

Cặp số (34, 51):

1 Phân tích ra thừa số nguyên tố:

• $34 = 2 \times 17$
  
• $51 = 3 \times 17$
  

ƯCLN(34, 51) = 17

BCNN(34, 51) = $2 \times 3 \times 17 = 102$

Cặp số (120, 70):

2 Phân tích ra thừa số nguyên tố:

• $120 = 2^3 \times 3 \times 5$
  
• $70 = 2 \times 5 \times 7$
  

ƯCLN(120, 70) = $2 \times 5 = 10$

BCNN(120, 70) = $2^3 \times 3 \times 5 \times 7 = 840$

Cặp số (15, 28):

3 Phân tích ra thừa số nguyên tố:

• $15 = 3 \times 5$
  
• $28 = 2^2 \times 7$
  

ƯCLN(15, 28) = 1

BCNN(15, 28) = $2^2 \times 3 \times 5 \times 7 = 420$

Cặp số (2987, 1):

4 Phân tích ra thừa số nguyên tố:

• $2987$ là số nguyên tố.
• $1$ không có thừa số nguyên tố.

ƯCLN(2987, 1) = 1

BCNN(2987, 1) = $2987$

Điền vào bảng:

So sánh tích ƯCLN(a, b) . BCNN(a, b) và a.b

Dựa vào bảng, ta có:

• $a \cdot b = 9 \times 12 = 108$
  
• $a \cdot b = 34 \times 51 = 1734$
  
• $a \cdot b = 120 \times 70 = 8400$
  
• $a \cdot b = 15 \times 28 = 420$
  
• $a \cdot b = 2987 \times 1 = 2987$
  

Ta thấy rằng:

$\text{ƯCLN}(a, b) \times \text{BCNN}(a, b) = a \times b$

Câu 2.46 trang 55 toán 6 kết nối tri thức

Tìm ƯCLN và BCNN của:

a) 3.52 và 52.7

b) 22.3.5; 32.7 và 3.5.11

Đáp án:

a) 3.5² và 5².7

+) Ta thấy các thừa số nguyên tố chung là 5 và thừa số nguyên tố riêng là 3 và 7

+) Số mũ nhỏ nhất của 5 là 2 nên ƯCLN cần tìm là 5² = 25

+) Số mũ lớn nhất của 3 là 1, số mũ lớn nhất của 5 là 2, số mũ lớn nhất của 7 là 1 nên BCNN cần tìm là 3.5².7 = 525

Vậy ƯCLN cần tìm là 5² = 25

BCNN cần tìm là 3.5².7  = 525.

b) 2².3.5; 3².7  và 3.5.11

• Ta thấy các thừa số nguyên tố chung là 3 và thừa số nguyên tố riêng là 2; 5; 7; 11
• Số mũ nhỏ nhất của 3 là 1 nên ƯCLN cần tìm là 3
• Số mũ lớn nhất của 2 là 2, số mũ lớn nhất của 3 là 2, số mũ lớn nhất của 5 là 1, số mũ lớn nhất của 7 là 1, số mũ lớn nhất của 11 là 1 nên BCNN cần tìm là 2².3².5.7.11 = 13 860

Vậy ƯCLN cần tìm là 3

BCNN cần tìm là 2².3².5.7.11 = 13 860.

Câu 2.47 trang 55 toán 6 kết nối tri thức

Các phân số sau đã tối giản chưa? Nếu chưa, hãy rút gọn về phân số tối giản.

a) 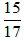                b) .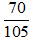

Đáp án: 

a) Vì ƯCLN(15, 17) = 1 nên phân số 15/17 là phân số tối giản.

b) Ta có: 70 = 2.7.5;  105= 3.5.7

+) Thừa số nguyên tố chung là 5 và 7

+ Số mũ nhỏ nhất của 5 là 1, số mũ nhỏ nhất của 7 là 1 nên ƯCLN(70, 105) = 35.

Do đó  70/105  không là phân số tối giản

• $\frac{70}{105} = \frac{70 \div 35}{105 \div 35} = \frac{2}{3}$
• Phân số $\frac{70}{105}$ khi rút gọn là $\frac{2}{3}$
  

vì ƯCLN(2, 3) = 1.

Câu 2.48 trang 55 toán 6 kết nối tri thức

Hai vận động viên chạy xung quanh một sân vận động. Hai vận động viên xuất phát tại cùng một thời điểm, cùng vị trí và chạy cùng chiều. Vận động viên thứ nhất chạy một vòng sân hết 360 giây, vận động viên thứ hai chạy một vòng sân mất 420 giây. Hỏi sau bao nhiêu phút họ lại gặp nhau, biết tốc độ di chuyển của họ không đổi?

Xem thêm>>> Giải toán 6 Bài 12 Bội chung. Bội chung nhỏ nhất trang 49 – KNTT

Đáp án: 

Bước 1: Phân tích thời gian mỗi vòng thành thừa số nguyên tố:

• $360 = 2^3 \times 3^2 \times 5$
  
• $420 = 2^2 \times 3 \times 5 \times 7$
  

Bước 2: Tìm BCNN của 360 và 420:

Chọn mỗi thừa số nguyên tố với số mũ lớn nhất từ mỗi phân tích:

• $2^3$= (từ 360)
• $3^2$= (từ 360)
• $5$ (từ cả 360 và 420)
• $7$ (từ 420)

BCNN của 360 và 420 là:

$$2^3\times 3^2\times 5\times 7=8\times 9\times 5\times 7=2520\text{ gi}\hat{\text{a}}\text{y}$$

Bước 3: Chuyển đổi giây thành phút:

$$2520 \text{ giây} \div 60 = 42 \text{ phút}$$Vậy, sau 42 phút, hai vận động viên sẽ lại gặp nhau tại điểm xuất phát.

Câu 2.49 trang 55 toán 6 kết nối tri thức

Quy đồng mẫu các phân số sau:

a)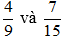

b)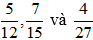

Đáp án: 

a) Quy đồng mẫu cho $\frac{4}{9}$ và $\frac{7}{15}$

Mẫu số của các phân số: 9 và 15.

• Phân tích ra thừa số nguyên tố:
  • $9 = 3^2$
    
  • $15 = 3 \times 5$
    

Tìm BCNN của 9 và 15:

• Sử dụng các thừa số nguyên tố với số mũ cao nhất: $3^2$và $5$
• $BCNN(9, 15) = 3^2 \times 5 = 45$.

Quy đồng mẫu số:

• $\frac{4}{9} = \frac{4 \times 5}{45} = \frac{20}{45}$
• $\frac{7}{15} = \frac{7 \times 3}{45} = \frac{21}{45}$

Kết quả sau khi quy đồng mẫu là $\frac{20}{45}$ và $\frac{21}{45}$.

b) Quy đồng mẫu cho $\frac{5}{12}$, $\frac{7}{15}$ và $\frac{4}{27}$

Mẫu số của các phân số: 12, 15 và 27.

• Phân tích ra thừa số nguyên tố:
  • $12 = 2^2 \times 3$
    
  • $15 = 3 \times 5$
    
  • $27 = 3^3$
    

Tìm BCNN của 12, 15 và 27:

• Sử dụng các thừa số nguyên tố với số mũ cao nhất: $2^2$, $3^3$ và $5$.
• $BCNN(12, 15, 27) = 2^2 \times 3^3 \times 5 = 4 \times 27 \times 5 = 540$.

Quy đồng mẫu số:

• $\frac{5}{12} = \frac{5 \times 45}{540} = \frac{225}{540}$
• $\frac{7}{15} = \frac{7 \times 36}{540} = \frac{252}{540}$
• $\frac{4}{27} = \frac{4 \times 20}{540} = \frac{80}{540}$$$​

Kết quả sau khi quy đồng mẫu là $\frac{225}{540}$, $\frac{252}{540}$ và $\frac{80}{540}$.

Câu 2.50 trang 55 toán 6 kết nối tri thức

Từ ba tấm gỗ có độ dài 56 dm, 48 dm và 40 dm, bác thợ mộc muốn cắt thành các thanh gỗ có độ dài như nhau mà không để thừa mẩu gỗ nào. Hỏi bác cắt như thế nào để được các thanh gỗ có độ dài lớn nhất có thể?

Đáp án: 

Bước 1: Phân tích mỗi số ra thừa số nguyên tố.

• $56 = 2^3 \times 7$
  
• $48 = 2^4 \times 3$
  
• $40 = 2^3 \times 5$
  

Bước 2: Tìm ƯCLN.

Lấy các thừa số nguyên tố chung với số mũ nhỏ nhất:

• Thừa số chung là $2$, và số mũ nhỏ nhất của $2$ trong các phân tích trên là $2^3$.

Vậy, $\text{ƯCLN}(56, 48, 40) = 2^3 = 8$.

Câu 2.51 trang 55 toán 6 kết nối tri thức

Học sinh lớp 6A khi xếp thành hàng 2, hàng 3, hàng 7 đều vừa đủ hàng. Hỏi số học sinh lớp 6A là bao nhiêu, biết rằng số học sinh nhỏ hơn 45.

Đáp án: 

Để tìm số học sinh lớp 6A, cần xác định số nhỏ nhất chia hết cho 2, 3, và 7 và đồng thời nhỏ hơn 45. Số này chính là bội chung nhỏ nhất (BCNN) của 2, 3, và 7.

Bước 1: Tìm BCNN của 2, 3 và 7

2, 3, và 7 là các số nguyên tố, vì vậy BCNN của chúng là tích của ba số này: $$BCNN(2, 3, 7) = 2 \times 3 \times 7 = 42$$

Bước 2: Xác định số học sinh trong lớp 6A

Số 42 là số nhỏ nhất chia hết cho 2, 3, và 7, và nó cũng nhỏ hơn 45.

Kết luận: Số học sinh trong lớp 6A là 42.

Câu 2.52 trang 55 toán 6 kết nối tri thức

Hai số có BCNN là 2³.3.5³ và ƯCLN là 2².5. Biết một trong hai số bằng 2².3.5, tìm số còn lại.

Đáp án: 

Gọi số cần tìm là x.

Tích của hai số đã cho là (2².3.5).x

Tích của BCNN và ƯCLN của hai số đã cho là:

( 2².3.5).(2².5) = (2³.2²).3.(5³.5) =2⁵.3.5⁴

Theo Bài tập 2.45, ta có tích của BCNN và ƯCLN của hai số tự nhiên bất kì thì bằng tích của hai số đó.

Do đó: ( 2².3.5). x = 2⁵.3.5⁴

x = (2⁵.3.5⁴) : (2².3.5)

x = (2⁵ : 2²).(3:3).(5⁴ : 5)

x = (2^5-2).1.5^4-1

x = 2³.5³

Vậy số cần tìm là 2³.5³.