Toán 7 Kết nối tri thức 1: Luyện tập chung trang 50

Phần Luyện tập chung trang 50 của sách giáo khoa Toán 7 Kết nối tri thức là một cơ hội tuyệt vời để học sinh củng cố và áp dụng những kiến thức đã học trong các bài trước. Trong bài viết này, chúng ta sẽ đi qua từng bài tập, phân tích kỹ lưỡng các phương pháp giải quyết và tìm hiểu cách thức những bài toán này giúp phát triển kỹ năng tư duy và giải quyết vấn đề, qua đó nâng cao hiểu biết và sự tự tin trong môn toán của học sinh.

Giải bài luyện tập chung trang 50

Bài 3.12 toán 7 sgk KNTT trang 50

Cho Hình 3.28.

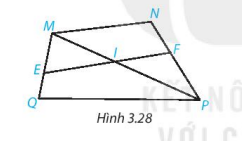
(a) Tìm các góc ở vị trí so le trong với góc \( \widehat{FIP} \); góc \( \widehat{NMI} \).
(b) Tìm các góc ở vị trí đồng vị với góc \( \widehat{EQP} \); góc \( \widehat{IFP} \).

Giải:

(a) Tìm các góc ở vị trí so le trong:
Góc \( \widehat{FIP} \) và góc \( \widehat{MPI} \) là hai góc so le trong vì đường thẳng \( FI \) cắt hai đường thẳng song song \( MN \) và \( PQ \).
Góc \( \widehat{NMI} \) và góc \( \widehat{MIF} \) là hai góc so le trong vì đường thẳng \( MI \) cắt hai đường thẳng song song \( MN \) và \( PQ \).

(b) Tìm các góc ở vị trí đồng vị:
Góc \( \widehat{EQP} \) và góc \( \widehat{FNM} \) là hai góc đồng vị vì đường thẳng \( QP \) cắt hai đường thẳng song song \( EQ \) và \( MN \).
Góc \( \widehat{IFP} \) và góc \( \widehat{NMI} \) là hai góc đồng vị vì đường thẳng \( IF \) cắt hai đường thẳng song song \( PQ \) và \( MN \).

Kết luận:
Các góc so le trong với góc \( \widehat{FIP} \) và góc \( \widehat{NMI} \) lần lượt là \( \widehat{MPI} \) và \( \widehat{MIF} \).
Các góc đồng vị với góc \( \widehat{EQP} \) và góc \( \widehat{IFP} \) lần lượt là \( \widehat{FNM} \) và \( \widehat{NMI} \).

Bài 3.13 toán 7 sgk KNTT trang 50

Cho Hình 3.29, biết \( \widehat{xAz} = 50^\circ \), \( \widehat{yBz} = 50^\circ \). Giải thích tại sao \( Ax \parallel By \).

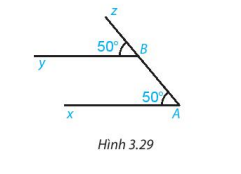
Giải:

Trong Hình 3.29, ta có:
\[
\widehat{xAz} = 50^\circ \quad \text{và} \quad \widehat{yBz} = 50^\circ.
\]

Vì hai góc \( \widehat{xAz} \) và \( \widehat{yBz} \) bằng nhau và nằm ở hai phía của đường thẳng \( z \), theo định lý về góc so le trong, nếu hai góc so le trong bằng nhau thì hai đường thẳng tạo thành các góc đó là song song.

Do đó, ta kết luận rằng:
\[
Ax \parallel By.
\]

Kết luận: Hai đường thẳng \( Ax \) và \( By \) song song vì chúng tạo thành các góc so le trong bằng nhau.

Xem thêm bài giải sau: “Toán 7 Kết nối tri thức 1: Hai đường thẳng song song và…“.

Bài 3.14 toán 7 sgk KNTT trang 50

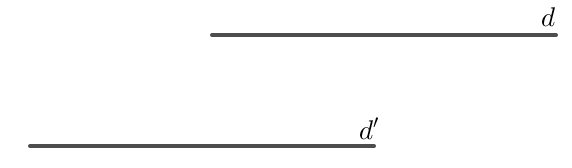
(a) Vẽ hai đường thẳng \( d \) và \( d’ \) sao cho \( d \parallel d’ \).
(b) Vẽ hai đoạn thẳng \( AB \) và \( CD \) sao cho \( CD = 2AB \) và \( CD \parallel AB \).

Giải:

(a) Để vẽ hai đường thẳng song song \( d \) và \( d’ \):
Bước 1: Vẽ đường thẳng \( d \).
Bước 2: Vẽ đường thẳng \( d’ \) sao cho nó song song với \( d \).

(b) Để vẽ hai đoạn thẳng \( AB \) và \( CD \) sao cho \( CD = 2AB \) và \( CD \parallel AB \):
Bước 1: Vẽ đoạn thẳng \( AB \) trên đường thẳng \( d \).
Bước 2: Vẽ đoạn thẳng \( CD \) trên đường thẳng \( d’ \), sao cho độ dài của \( CD \) gấp đôi độ dài của \( AB \), và đoạn thẳng \( CD \) song song với đoạn thẳng \( AB \).

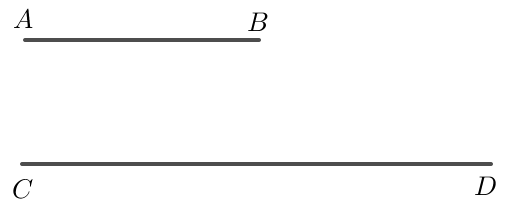
Kết luận: Hình đã được vẽ theo yêu cầu với các đoạn thẳng và đường thẳng song song và có tỷ lệ thích hợp.

Bài 3.15 toán 7 sgk KNTT trang 50

Cho Hình 3.30, biết các góc \( \widehat{MNQ} \) và \( \widehat{PQN} \) có cùng số đo bằng \( 35^\circ \). Chứng tỏ \( MN \parallel QP \).

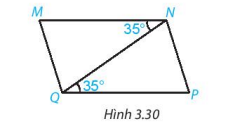
Giải:

Dựa vào Hình 3.30, ta có:
\[
\widehat{MNQ} = 35^\circ \quad \text{và} \quad \widehat{PQN} = 35^\circ.
\]

Hai góc \( \widehat{MNQ} \) và \( \widehat{PQN} \) là hai góc so le trong được tạo bởi đường thẳng \( MN \) cắt hai đường thẳng \( QP \) và đường thẳng chứa đoạn \( NQ \).

Theo định lý về góc so le trong, nếu hai góc so le trong bằng nhau thì hai đường thẳng song song. Do đó, ta có:
\[
MN \parallel QP.
\]

Kết luận: Vì \( \widehat{MNQ} = \widehat{PQN} \), nên \( MN \parallel QP \) theo tính chất của góc so le trong.

Bài 3.16 toán 7 sgk KNTT trang 50

Cho đoạn thẳng \( AB \). Vẽ hai tia \( Ax \), \( By \) sao cho chúng tạo với \( AB \) hai góc so le trong có cùng số đo bằng \( 60^\circ \) (\( \widehat{xAB} = \widehat{yBA} = 60^\circ \)). Trên hình vừa vẽ, hai đường thẳng chứa hai tia \( Ax \) và \( By \) có song song với nhau không? Vì sao?

Giải:

Vẽ hai tia \( Ax \) và \( By \) sao cho chúng tạo với \( AB \) hai góc so le trong bằng nhau, cụ thể là \( \widehat{xAB} = 60^\circ \) và \( \widehat{yBA} = 60^\circ \).
Theo tính chất của góc so le trong, nếu hai góc so le trong bằng nhau, thì hai đường thẳng chứa hai tia đó phải song song.

Do đó, hai đường thẳng chứa các tia \( Ax \) và \( By \) song song với nhau.

Kết luận: Hai đường thẳng chứa tia \( Ax \) và \( By \) song song với nhau vì chúng tạo với đoạn thẳng \( AB \) hai góc so le trong bằng nhau.