Khái niệm về hai đường thẳng song song và… là một trong những nền tảng cơ bản nhất trong hình học, và việc nắm vững nó sẽ mở ra cánh cửa cho nhiều bài toán phức tạp hơn. Trong phần này của sách giáo khoa Toán 7 Kết nối tri thức, chúng ta sẽ khám phá chi tiết về hai đường thẳng song song, cách nhận biết và những tính chất quan trọng liên quan, giúp học sinh xây dựng một nền tảng vững chắc cho những chủ đề toán học sắp tới.
Giải bài hai đường thẳng song song và dấu hiệu nhận biết
Bài 3.6 toán 7 sgk KNTT trang 49
Quan sát Hình 3.24.
(a) Tìm một góc ở vị trí so le trong với góc \( \angle MNB \).
(b) Tìm một góc ở vị trí đồng vị với góc \( \angle ACB \).
(c) Kể tên một cặp góc trong cùng phía.
(d) Biết \( MN \parallel BC \), em hãy kể tên ba cặp góc bằng nhau trong hình vẽ.
Giải:
(a) Một góc ở vị trí so le trong với góc \( \angle MNB \) là \( \angle ABC \). Vì \( MN \parallel BC \) và đường thẳng \( AN \) cắt hai đường thẳng song song này, nên \( \angle MNB \) và \( \angle ABC \) là hai góc so le trong.
(b) Một góc ở vị trí đồng vị với góc \( \angle ACB \) là \( \angle AMN \). Vì \( MN \parallel BC \) và đường thẳng \( AC \) cắt hai đường thẳng song song này, nên \( \angle ACB \) và \( \angle AMN \) là hai góc đồng vị.
(c) Một cặp góc trong cùng phía là \( \angle MNB \) và \( \angle ACB \). Hai góc này nằm ở cùng phía của đường thẳng cắt hai đường thẳng song song \( MN \) và \( BC \).
(d) Vì \( MN \parallel BC \), ta có ba cặp góc bằng nhau trong hình vẽ:
\( \angle MNB = \angle ABC \) (So le trong)
\( \angle AMN = \angle ACB \) (Đồng vị)
\( \angle MAN = \angle BAC \) (Đồng vị)
Kết luận:
Góc so le trong với \( \angle MNB \) là \( \angle ABC \).
Góc đồng vị với \( \angle ACB \) là \( \angle AMN \).
Một cặp góc trong cùng phía là \( \angle MNB \) và \( \angle ACB \).
Ba cặp góc bằng nhau trong hình vẽ là \( \angle MNB = \angle ABC \), \( \angle AMN = \angle ACB \), và \( \angle MAN = \angle BAC \).
Bài 3.7 toán 7 sgk KNTT trang 49
Quan sát Hình 3.25. Biết \( \widehat{MEF} = 40^\circ \), \( \widehat{EMN} = 40^\circ \). Em hãy giải thích tại sao \( EF \parallel NM \).
Giải:
Dựa vào hình vẽ và các số đo góc đã cho:
Ta có \( \widehat{MEF} = 40^\circ \) và \( \widehat{EMN} = 40^\circ \).
Góc \( \widehat{MEF} \) và góc \( \widehat{EMN} \) là hai góc so le trong do đường thẳng \( EF \) cắt hai đường thẳng \( MN \) và \( EM \).
Theo tính chất của các góc so le trong, nếu hai góc so le trong bằng nhau thì hai đường thẳng tạo thành các góc đó song song với nhau.
Vì \( \widehat{MEF} = \widehat{EMN} \), nên theo tính chất của góc so le trong, ta kết luận rằng:
\[
EF \parallel NM.
\]
Kết luận: Do \( \widehat{MEF} = \widehat{EMN} \), ta có \( EF \parallel NM \) theo tính chất của góc so le trong.
Cùng tham khảo bài giải sau: “Toán 7 Kết nối tri thức 1: Góc ở vị trí đặc biệt. Tia phân…“.
Bài 3.8 toán 7 sgk KNTT trang 49
Quan sát Hình 3.26, giải thích tại sao \( AB \parallel DC \).
Giải:
Trong Hình 3.26, tứ giác \( ABCD \) có hai góc vuông tại các điểm \( A \) và \( D \):
\[
\widehat{A} = \widehat{D} = 90^\circ.
\]
Do đó, các đoạn thẳng \( AB \) và \( DC \) đều vuông góc với đường thẳng \( AD \).
Theo tính chất của hai đường thẳng cùng vuông góc với một đường thẳng thứ ba, nếu hai đường thẳng cùng vuông góc với một đường thẳng thì chúng song song với nhau.
Vì \( AB \) và \( DC \) cùng vuông góc với \( AD \), nên ta kết luận rằng:
\[
AB \parallel DC.
\]
Kết luận: Hai đường thẳng \( AB \) và \( DC \) song song với nhau vì chúng cùng vuông góc với đường thẳng \( AD \).
Bài 3.9 toán 7 sgk KNTT trang 49
Cho điểm \( A \) và đường thẳng \( d \) không đi qua \( A \). Hãy vẽ đường thẳng \( d’ \) đi qua \( A \) và song song với \( d \).
Giải:
Để vẽ đường thẳng \( d’ \) đi qua điểm \( A \) và song song với đường thẳng \( d \), ta có các bước sau:
Bước 1: Xác định vị trí của điểm \( A \), sao cho điểm này không nằm trên đường thẳng \( d \).
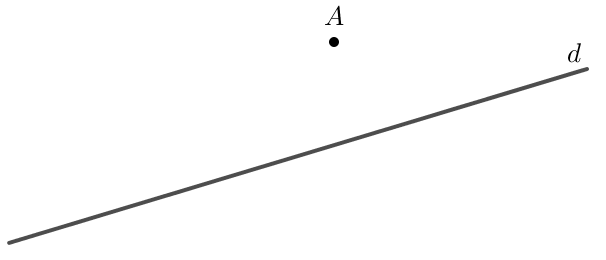
Bước 2: Vẽ một đường thẳng \( d’ \) đi qua điểm \( A \) và có hướng song song với đường thẳng \( d \).
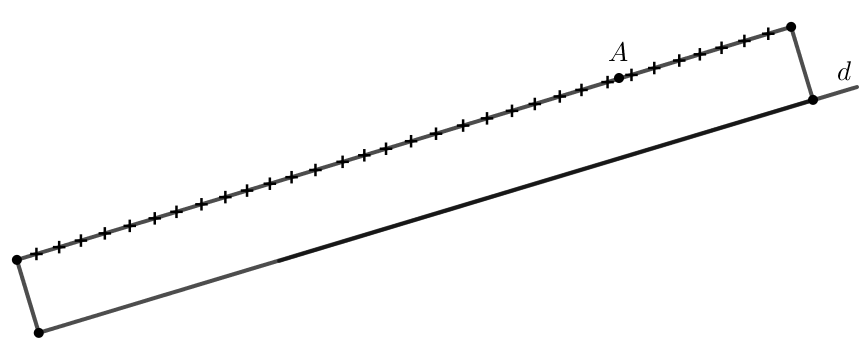
Bước 3: Đường thẳng \( d’ \) chính là đường thẳng cần tìm, vì nó đi qua điểm \( A \) và song song với \( d \).
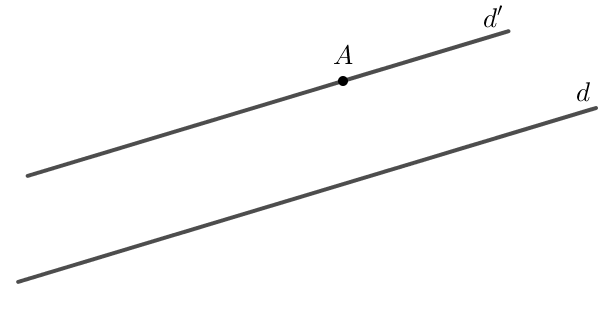
Kết luận: Đường thẳng \( d’ \) đi qua điểm \( A \) và song song với đường thẳng \( d \) đã được vẽ ở hình trên.
Bài 3.10 toán 7 sgk KNTT trang 49
Cho hai điểm \( A \) và \( B \). Hãy vẽ đường thẳng \( a \) đi qua \( A \) và đường thẳng \( b \) đi qua \( B \) sao cho \( a \parallel b \).
Giải:
Để vẽ hai đường thẳng song song \( a \) và \( b \), ta thực hiện các bước sau:
Bước 1: Xác định vị trí của điểm \( A \) và vẽ đường thẳng \( a \) đi qua điểm \( A \).
Bước 2: Xác định vị trí của điểm \( B \) và vẽ đường thẳng \( b \) đi qua điểm \( B \) sao cho đường thẳng này song song với đường thẳng \( a \).
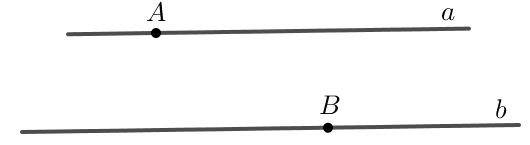
Bước 3: Do \( a \parallel b \), hai đường thẳng này sẽ không cắt nhau tại bất kỳ điểm nào.
Kết luận: Hai đường thẳng \( a \) và \( b \) đã được vẽ sao cho \( a \parallel b \), với \( a \) đi qua điểm \( A \) và \( b \) đi qua điểm \( B \).
Bài 3.11 toán 7 sgk KNTT trang 49
Hãy vẽ hai đoạn thẳng \( AB \) và \( MN \) sao cho \( AB \parallel MN \) và \( AB = MN \).
Giải:
Để vẽ hai đoạn thẳng \( AB \) và \( MN \) sao cho \( AB \parallel MN \) và \( AB = MN \), ta thực hiện các bước sau:
Bước 1: Vẽ đoạn thẳng \( AB \) với chiều dài cố định.
Bước 2: Vẽ đoạn thẳng \( MN \) với cùng chiều dài với đoạn thẳng \( AB \) và song song với đoạn thẳng \( AB \).

Bước 3: Hai đoạn thẳng \( AB \) và \( MN \) sẽ không giao nhau vì chúng song song với nhau và có cùng chiều dài.
Kết luận: Hai đoạn thẳng \( AB \) và \( MN \) đã được vẽ sao cho \( AB \parallel MN \) và \( AB = MN \).








