Hiểu và áp dụng các định lí toán học là một kỹ năng quan trọng không chỉ trong học tập mà còn trong cuộc sống. Trong phần ‘Định lí và chứng minh định lí‘ của sách giáo khoa Toán 7 Kết nối tri thức, chúng ta sẽ tìm hiểu về cách xây dựng và chứng minh các định lí toán học, từ đó giúp học sinh phát triển tư duy logic và khả năng giải quyết vấn đề. Bài viết này sẽ hướng dẫn các em cách tiếp cận các định lí, hiểu bản chất của chúng và áp dụng vào việc giải các bài toán phức tạp.
Giải bài định lí và chứng minh định lí
Bài 3.24 toán 7 sgk KNTT trang 57
Có thể coi định lý “Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau” được suy ra trực tiếp từ định lý về dấu hiệu nhận biết hai đường thẳng song song không? Suy ra như thế nào?
Giải:
Định lý về dấu hiệu nhận biết hai đường thẳng song song được phát biểu như sau: “Nếu hai đường thẳng cắt bởi một đường thẳng thứ ba mà có hai góc so le trong bằng nhau thì hai đường thẳng đó song song với nhau.”
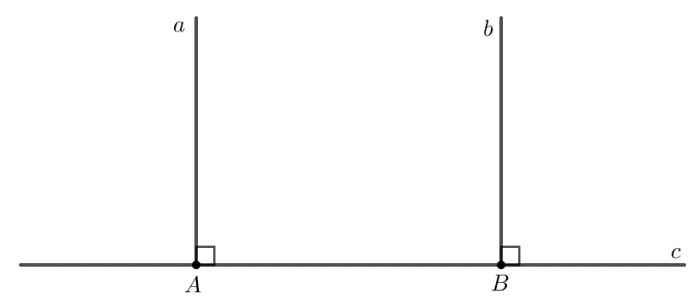
Bây giờ, hãy xem xét hai đường thẳng phân biệt \( d_1 \) và \( d_2 \) cùng vuông góc với một đường thẳng thứ ba \( d_3 \).
Giả sử \( d_1 \perp d_3 \) và \( d_2 \perp d_3 \). Điều này có nghĩa là các góc giữa \( d_1 \) và \( d_3 \), cũng như giữa \( d_2 \) và \( d_3 \), đều bằng \( 90^\circ \).
Theo định lý về góc so le trong, nếu hai góc so le trong bằng nhau thì hai đường thẳng là song song. Ở đây, hai góc vuông này đóng vai trò của hai góc so le trong, vì vậy, ta có thể suy ra rằng \( d_1 \parallel d_2 \).
Do đó, ta có thể suy ra trực tiếp từ định lý về dấu hiệu nhận biết hai đường thẳng song song rằng “Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.”
Kết luận: Định lý về hai đường thẳng vuông góc với một đường thẳng thứ ba có thể được suy ra trực tiếp từ định lý về dấu hiệu nhận biết hai đường thẳng song song.
Bài 3.25 toán 7 sgk KNTT trang 57
Hãy chứng minh định lý nói ở Ví dụ trang 56: “Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại.” Trong chứng minh đó ta đã sử dụng những điều đúng đã biết nào?
Giải:
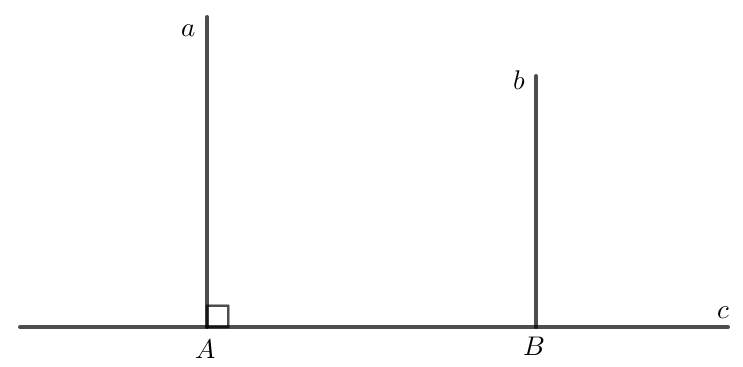
Xét hai đường thẳng song song \( d_1 \parallel d_2 \) và đường thẳng \( d_3 \) vuông góc với đường thẳng \( d_1 \) tại một điểm \( A \), tức là \( d_3 \perp d_1 \).
Giả sử \( d_3 \perp d_1 \) tại điểm \( A \). Ta cần chứng minh rằng \( d_3 \perp d_2 \) tại điểm \( B \).
Sử dụng định lý về tính chất của hai đường thẳng song song, ta biết rằng nếu một đường thẳng cắt hai đường thẳng song song thì các góc so le trong được tạo thành bằng nhau.
Do đó, góc giữa \( d_3 \) và \( d_2 \) tại điểm \( B \) cũng phải bằng \( 90^\circ \). Điều này có nghĩa là \( d_3 \) vuông góc với \( d_2 \).
Từ đó suy ra rằng, nếu \( d_3 \perp d_1 \) thì \( d_3 \perp d_2 \) vì cả hai đường thẳng \( d_1 \) và \( d_2 \) song song với nhau.
Kết luận: Sử dụng định lý về góc so le trong và định lý về các góc vuông, ta có thể suy ra rằng một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại.
Xem thêm: “Toán 7 Kết nối tri thức 1: Tiên đề Euclid…thẳng song song“.
Bài 3.26 toán 7 sgk KNTT trang 57
Cho góc \( xOy \) không phải là góc bẹt. Khẳng định nào sau đây là đúng?
(1) Nếu \( Ot \) là tia phân giác của góc \( xOy \) thì \( \widehat{xOt} = \widehat{tOy} \).
(2) Nếu tia \( Ot \) thỏa mãn \( \widehat{xOt} = \widehat{tOy} \) thì \( Ot \) là tia phân giác của góc \( xOy \).
Nếu có khẳng định không đúng, hãy nêu ví dụ cho thấy khẳng định đó không đúng. (Gợi ý: Xét tia đối của một tia phân giác).
Giải:
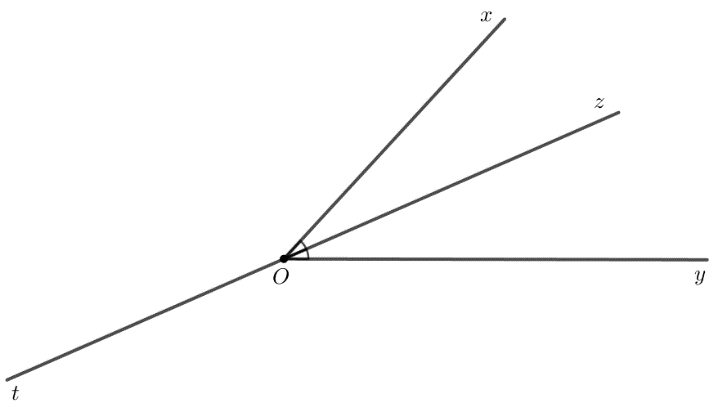
(1) Khẳng định (1): Đúng.
Giả sử \( Ot \) là tia phân giác của góc \( xOy \), theo định nghĩa của tia phân giác, tia này chia góc \( xOy \) thành hai góc bằng nhau. Do đó, ta có:
\[
\widehat{xOt} = \widehat{tOy}.
\]
Vì vậy, khẳng định (1) là đúng.
(2) Khẳng định (2): Sai.
Ta cần đưa ra một ví dụ cho thấy khẳng định này không đúng.
Giả sử tia \( Ot \) thỏa mãn \( \widehat{xOt} = \widehat{tOy} \), nhưng \( Ot \) không phải là tia phân giác của góc \( xOy \). Ta xét tia đối của tia phân giác \( Ot \), tức là tia \( Ot’ \) kéo dài theo hướng ngược lại của tia phân giác. Khi đó, ta cũng có \( \widehat{xOt’} = \widehat{t’Oy} \), nhưng \( Ot’ \) không phải là tia phân giác của góc \( xOy \).
Điều này chứng minh rằng khẳng định (2) không phải lúc nào cũng đúng.
Kết luận:
Khẳng định (1) đúng: Nếu \( Ot \) là tia phân giác của góc \( xOy \), thì \( \widehat{xOt} = \widehat{tOy} \).
Khẳng định (2) sai: Ngay cả khi \( \widehat{xOt} = \widehat{tOy} \), \( Ot \) không nhất thiết phải là tia phân giác của góc \( xOy \) (ví dụ tia đối của tia phân giác cũng thỏa mãn điều kiện này).








