Toán 7 Kết nối tri thức 1: Bài tập cuối chương 3

Bài tập cuối chương 3 trong sách giáo khoa Toán 7 Kết nối tri thức là cơ hội quan trọng để học sinh ôn tập và kiểm tra lại những kiến thức đã học trong suốt chương. Trong bài viết này, chúng ta sẽ đi qua các bài tập này, khám phá các mẹo và phương pháp hiệu quả để giải quyết chúng, giúp các em học sinh không chỉ củng cố kiến thức mà còn phát triển kỹ năng giải toán, đảm bảo sự sẵn sàng cho các thử thách tiếp theo trong học tập.

Giải bài tập cuối chương 3

Bài 3.32 toán 7 sgk KNTT trang 59

Chứng minh rằng: Cho điểm \( A \) và đường thẳng \( d \) thì có duy nhất đường thẳng đi qua \( A \) vuông góc với \( d \), tức là nếu có hai đường thẳng đi qua \( A \) vuông góc với \( d \) thì chúng phải trùng nhau.

Giải:

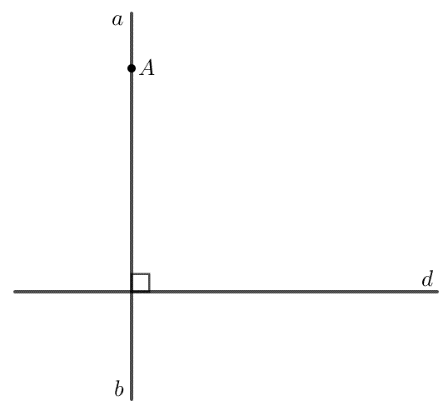
Chứng minh:

Giả sử có hai đường thẳng \( a \) và \( b \) đều đi qua điểm \( A \) và vuông góc với đường thẳng \( d \).

Ta có:
\[
\widehat{a \perp d} = \widehat{b \perp d} = 90^\circ.
\]

Do đó, hai đường thẳng \( a \) và \( b \) cùng đi qua một điểm \( A \) và tạo với \( d \) các góc vuông bằng nhau. Theo định nghĩa của góc vuông, chỉ có một đường thẳng duy nhất đi qua một điểm \( A \) và vuông góc với một đường thẳng cho trước.

Vì vậy, hai đường thẳng \( a \) và \( b \) phải trùng nhau.

Kết luận: Có duy nhất một đường thẳng đi qua điểm \( A \) và vuông góc với đường thẳng \( d \).

Bài 3.33 toán 7 sgk KNTT trang 59

Vẽ ba đường thẳng phân biệt \( a \), \( b \), \( c \) sao cho \( a \parallel b \), \( b \parallel c \) và hai đường thẳng phân biệt \( m \), \( n \) cùng vuông góc với \( a \). Hỏi trên hình có bao nhiêu cặp đường thẳng song song, có bao nhiêu cặp đường thẳng vuông góc?

Giải:

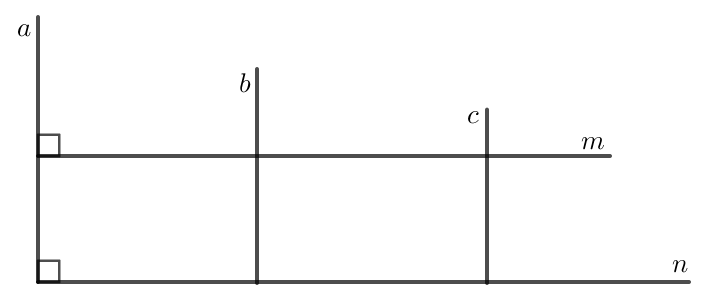
Số cặp đường thẳng song song:
Các cặp đường thẳng song song gồm: \( a \parallel b \), \( b \parallel c \), và \( a \parallel c \).
Do đó, có tổng cộng 3 cặp đường thẳng song song.

Số cặp đường thẳng vuông góc:
Các cặp đường thẳng vuông góc gồm: \( a \perp m \), \( a \perp n \), \( b \perp m \), \( b \perp n \), \( c \perp m \), và \( c \perp n \).
Do đó, có tổng cộng 6 cặp đường thẳng vuông góc.

Kết luận: Trên hình có 3 cặp đường thẳng song song và 6 cặp đường thẳng vuông góc.

Xem thêm bài sau: “Toán 7 Kết nối tri thức 1: Luyện tập chung trang 58“.

Bài 3.34 toán 7 sgk KNTT trang 59

Cho Hình 3.50, trong đó hai tia \( Ax \) và \( By \) nằm trên hai đường thẳng song song. Chứng minh rằng \( \widehat{C} = \widehat{A} + \widehat{B} \).

Giải:

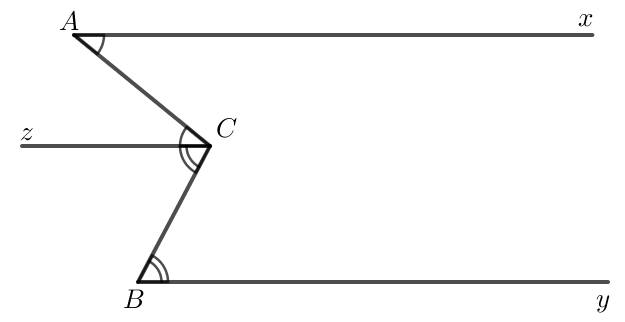
Chứng minh:

Ta có hai đường thẳng song song \( x \parallel y \), với các tia \( Ax \) và \( By \) lần lượt nằm trên các đường thẳng này.

Xét tam giác \( ABC \), ta có:
\[
\widehat{C} = \widehat{A} + \widehat{B}
\]
theo tính chất tổng các góc trong tam giác.

Như vậy, ta đã chứng minh được rằng:
\[
\widehat{C} = \widehat{A} + \widehat{B}.
\]

Kết luận: Dựa trên hình học tam giác và tính chất của góc trong tam giác, ta có \( \widehat{C} = \widehat{A} + \widehat{B} \).

Bài 3.35 toán 7 sgk KNTT trang 59

Cho Hình 3.51, trong đó \( Ox \) và \( Ox’ \) là hai tia đối nhau.

Giải:

(a) Vì \( Ox \) và \( Ox’ \) là hai tia đối nhau, tổng các góc \( \widehat{O_1} + \widehat{O_2} + \widehat{O_3} \) sẽ bằng 180 độ, do các tia \( Ox \), \( Oy \), và \( Oz \) tạo thành một đường thẳng.

Do đó:
\[
\widehat{O_1} + \widehat{O_2} + \widehat{O_3} = 180^\circ.
\]

(b) Từ công thức tổng ba góc, ta có:
\[
\widehat{O_2} = 180^\circ – (\widehat{O_1} + \widehat{O_3}).
\]

Thay giá trị của \( \widehat{O_1} \) và \( \widehat{O_3} \):
\[
\widehat{O_2} = 180^\circ – (60^\circ + 70^\circ) = 50^\circ.
\]

Kết luận: Tổng ba góc tại điểm \( O \) bằng 180 độ, và khi biết hai góc, ta có thể tính được góc còn lại.

Bài 3.36 toán 7 sgk KNTT trang 59

Cho Hình 3.52, biết \( \widehat{xOy} = 120^\circ \) và \( \widehat{yOz} = 110^\circ \). Tính số đo góc \( \widehat{zOx} \).

Gợi ý: Kẻ thêm tia đối của tia \( Oy \).

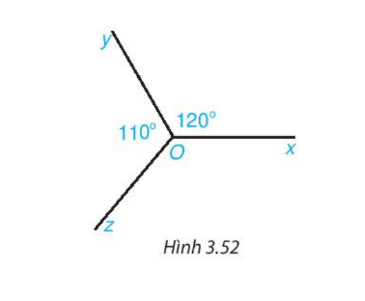
Giải:

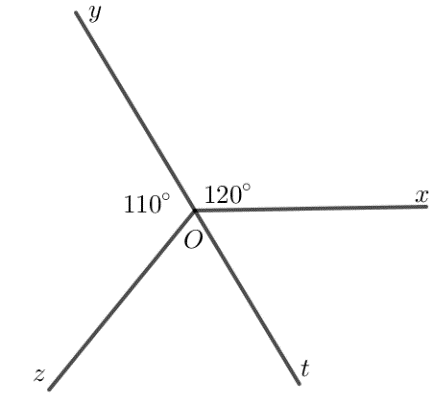
Tổng ba góc tạo bởi các tia \( Ox \), \( Oy \), và \( Oz \) tại điểm \( O \) trên mặt phẳng là 360 độ.

Do đó, ta có phương trình:
\[
\widehat{xOy} + \widehat{yOz} + \widehat{zOx} = 360^\circ.
\]

Thay các giá trị của \( \widehat{xOy} \) và \( \widehat{yOz} \) vào phương trình:
\[
120^\circ + 110^\circ + \widehat{zOx} = 360^\circ.
\]

Từ đó, tính được \( \widehat{zOx} \):
\[
\widehat{zOx} = 360^\circ – (120^\circ + 110^\circ) = 130^\circ.
\]

Kết luận: Số đo góc \( \widehat{zOx} \) là \( 130^\circ \).