Giải toán 6 Bài 9 Dấu hiệu chia hết trang 34 – Kết nối tri thức

Trang 34 của sách Giải Toán 6 – Bài 9 Dấu hiệu chia hết cung cấp các dấu hiệu cơ bản giúp học sinh nhận biết số chia hết cho các số như 2, 3, 5, 9 và nhiều số khác. Bài học giải thích cách áp dụng các quy tắc chia hết thông qua các ví dụ và bài tập cụ thể, giúp học sinh nắm vững phương pháp và áp dụng vào giải toán hiệu quả.

Giải toán 6 Bài 9 Dấu hiệu chia hết trang 34

Câu 2.10 trang 37 toán 6 kết nối tri thức

Trong các số sau, số nào chia hết cho 2, số nào chia hết cho 5?

324; 248; 2 020; 2025.

Đáp án: 

Kiểm tra các số:

1. 324:
   • Chữ số hàng đơn vị là 4 (chia hết cho 2).
   • Chữ số hàng đơn vị không phải là 0 hoặc 5 (không chia hết cho 5).
2. 248:
   • Chữ số hàng đơn vị là 8 (chia hết cho 2).
   • Chữ số hàng đơn vị không phải là 0 hoặc 5 (không chia hết cho 5).
3. 2,020:
   • Chữ số hàng đơn vị là 0 (chia hết cho 2).
   • Chữ số hàng đơn vị là 0 (chia hết cho 5).
4. 2,025:
   • Chữ số hàng đơn vị là 5 (không chia hết cho 2).
   • Chữ số hàng đơn vị là 5 (chia hết cho 5).

Câu 2.11 trang 37 toán 6 kết nối tri thức

Trong các số sau, số nào chia hết cho 3, số nào chia hết cho 9?

450 ; 123 ; 2 019 ; 2 025.

Đáp án: 

Kiểm tra các số:

1. 450:
   • Tổng các chữ số: $4 + 5 + 0 = 9$ (chia hết cho 3 và 9).
2. 123:
   • Tổng các chữ số: $1 + 2 + 3 = 6$ (chia hết cho 3, không chia hết cho 9).
3. 2,019:
   • Tổng các chữ số: $2 + 0 + 1 + 9 = 12$ (chia hết cho 3, không chia hết cho 9).
4. 2,025:
   • Tổng các chữ số: $2 + 0 + 2 + 5 = 9$ (chia hết cho 3 và 9).

Câu 2.12 trang 37 toán 6 kết nối tri thức

Khối lớp 6 của một trường có 290 học sinh đi dã ngoại. Cô phụ trách muốn chia đều số học sinh của khối 6 thành 9 nhóm. Hỏi cô chia nhóm được như vậy không?

Đáp án: 

Để kiểm tra xem số học sinh có thể chia đều thành 9 nhóm hay không, ta cần kiểm tra xem 290 có chia hết cho 9 hay không.

• Tính: $290 \div 9 = 32.222$ (không chia hết cho 9)

Vì $290$ không chia hết cho $9$, nên không thể chia đều 290 học sinh thành 9 nhóm mà mỗi nhóm có số học sinh bằng nhau.

Câu 2.13 trang 37 toán 6 kết nối tri thức

Có 162 học sinh tham gia chương trình đào tạo bóng đá, được chia thành các đội. Mỗi đội cần có 9 học sinh. Hỏi có đội nào không đủ 9 học sinh hay không?

Đáp án: 

Tổng các chữ số của 162 là 1 + 6 + 2 = 9 chia hết cho 9 nên 162 chia hết cho 9. Do đó chia 162 em học sinh thành các đội, thì không có đội nào không đủ 9 học sinh.

Câu 2.14 trang 37 toán 6 kết nối tri thức

Thay dấu * bởi một chữ số để số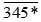  

a) Chia hết cho 2

b) Chia hết cho 3

c) Chia hết cho 5

d) Chia hết cho 9.

Đáp án: 

Điều kiện * ∈ N, 0 ≤ * ≤ 9

a) Số 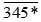chia hết cho 2 thì nó phải có tận cùng là chữ số chẵn nên * ∈ {0;2;4;6;8}

Vậy có thể thay * bằng các chữ số: 0; 2; 4; 6; 8

b) Số 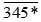 chia hết cho 3 thì tổng các chữ số của nó cũng chia hết cho 3.

Do đó 3 + 4 + 5 + * = 12 + * chia hết cho 3.

Mà 12 chia hết cho 3 nên * cũng phải chia hết cho 3 nên * ∈ {0;3;6;9}

Vậy có thể thay * bằng các chữ số: 0; 3; 6; 9

c) Số 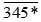 chia hết cho 5 thì nó phải có tận cùng là 0 hoặc 5 nên * ∈ {0;5}

Vậy có thể thay * bằng các chữ số: 0 ; 5

d) Số 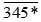chia hết cho 9 thì tổng các chữ số của nó cũng chia hết cho 9

Do đó 3 + 4 + 5 + * = 12 + * chia hết cho 9 nên * ∈ {6}

Vậy có thể thay * bằng chữ số 6.

Xem thêm>>> Giải toán 6 Bài 8 Quan hệ chia hết và tính chất trang 33 – KNTT

Câu 2.15 trang 37 toán 6 kết nối tri thức

Dùng 3 chữ số 3, 0, 4 hãy viết các số tự nhiên có ba chữ số khác nhau và thỏa mãn một trong hai điều kiện:

a) Các số đó chia hết cho 2

b) Các số đó chia hết cho 5

Đáp án: 

a) Để tìm số tự nhiên chia hết cho 2, chữ số tận cùng của số đó phải là 0 hoặc 4.

• Với chữ số tận cùng là 0: Các số có ba chữ số khác nhau là: 340, 430.
• Với chữ số tận cùng là 4: Chữ số 0 không thể đứng ở hàng trăm, nên số 0 phải ở hàng chục. Do đó, số có ba chữ số khác nhau là: 304.

Vậy, các số chia hết cho 2 là: 304, 340, 430.

b) Để tìm số tự nhiên chia hết cho 5, chữ số tận cùng của số đó phải là 0.

Với các chữ số 3, 0, 4, và yêu cầu số tự nhiên có ba chữ số khác nhau, ta có các số: 340, 430.

Vậy, các số chia hết cho 5 là: 340, 430.

Câu 2.16 trang 37 toán 6 kết nối tri thức

Từ các chữ số 5, 0, 4, 2 viết các số tự nhiên có ba chữ số khác nhau sao cho mỗi số đó chia hết cho 3.

Đáp án: 

Để tìm các số tự nhiên có ba chữ số khác nhau từ các chữ số 5, 0, 4, 2 mà chia hết cho 3, ta thực hiện các bước sau:

Tính tổng của các chữ số 5, 0, 4, 2: $5 + 0 + 4 + 2 = 11$.

Chọn ba chữ số và kiểm tra tổng chia hết cho 3:

• • 502: $5 + 0 + 2 = 7$ (không chia hết cho 3)
  • 520: $5 + 2 + 0 = 7$ (không chia hết cho 3)
  • 504: $5 + 0 + 4 = 9$ (chia hết cho 3)
  • 450: $4 + 5 + 0 = 9$ (chia hết cho 3)
  • 452: $4 + 5 + 2 = 11$ (không chia hết cho 3)
  • 420: $4 + 2 + 0 = 6$ (chia hết cho 3)
  • 204: $2 + 0 + 4 = 6$ (chia hết cho 3)
  • 240: $2 + 4 + 0 = 6$ (chia hết cho 3)

Các số thỏa mãn điều kiện là: 504, 450, 420, 204, 240.